縱觀中級財務管理整本書，算的就是現金流，玩的就是折現。今天的一塊錢是否等于明天的一塊錢，用貨幣時間價值的思路就能回答。

一、貨幣時間價值

今天的一塊錢為什么比明天的一塊錢更值錢，因為今天的一塊錢可以拿去投資和再投資。

上述圖示就是貨幣時間價值的含義。是指在沒有風險和沒有通貨膨脹的情況下，貨幣經歷一定時間的投資和再投資所增加的價值。

（一）衡量指標

通常使用相對數表示貨幣的時間價值，即用增加的價值占投入貨幣的百分數來表示，用相對數表示的貨幣時間價值也稱為純粹利率（簡稱純利率）。

【注意】通過貨幣時間價值的含義，我們可以知道：

（1）純利率是在沒有通貨膨脹、無風險情況下資金市場的平均利率。

（2）沒有通貨膨脹時，短期國庫券的利率可以視為純利率（以國家信譽作保障，視為無風險利率）。

（二）作用：將某一時點的貨幣價值金額折算為其他時點的價值金額。

基于此，不同時點的貨幣不再具有可比性，要進行比較，必須轉化到同一時點。

也就是說，如果要將今天的一塊錢和明天的一塊錢作比較，就必須把明天的一塊錢折現到今天。既然今天的一塊錢＞明天的一塊錢，我們就可以知道，折現的過程是一個“縮水”的過程。

接下來，我們來講折現（現值）和終值。

二、復利終值和現值（解決一次性款項的問題）

【注意】復利是一個算次方的問題，而單利是一個乘法問題。即：

現存入本金100元，銀行存款利率是8%，問三年后連本帶利能從銀行取出多少錢？

單利計息：能取出的金額=本金×（1+利率×期數）=100×（1+8%×3）=124（該思路在后續的學習中能用到，比如到期一次還本付息的債券）。

【提示】但是折現只能用復利折現。

三、年金終值和現值（等額、等距）

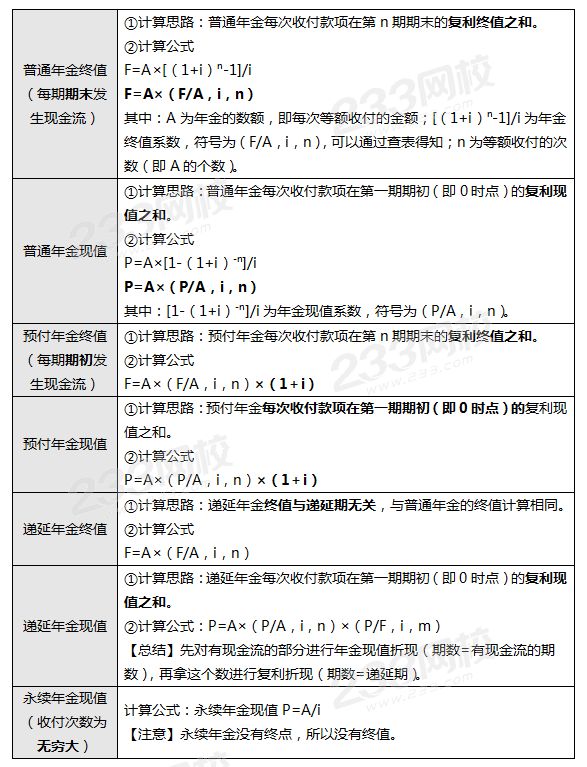
四、年償債基金和年資本回收額

（一）年償債基金

（二）年資本回收額

五、練一練