（一）排列問題：從個元素中取個元素，需要考慮的順序，用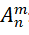表示。

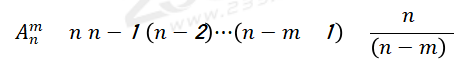
注意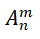：只表示排列數，而不表示具體的排列。

補充：規定0  1

基本排列問題例題

在某市物理競賽中，一中、二中、三中三所學校分別有3名、2名、1名同學獲得一等獎，將這6名同學排成一排合影，要求來自同一個學校的學生站在一起，則不同的排法共有（??）種。

A. 12 B. 36 C. 72 D. 120 E. 720

【答案】C

（二）組合問題：從個元素中取個元素，無需考慮的順序，用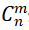表示。

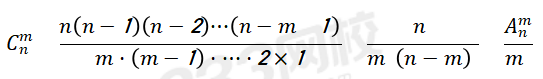
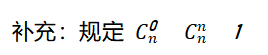
基本組合問題例題

飛騰公司近期組織員工出差培訓，每回去兩個人，從甲、乙、丙、丁、戊、己中任選兩人出行，那么共有（??）種不同的方案。

A. 5 B. 10 C. 15 D. 20 E. 25

【答案】C

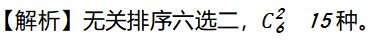
加法原理：完成一件事共有類辦法；在第一類辦法中有種不同的方法，在第二類辦法中有種不同的方法，…在第類辦法中有種不同的方法；那么完成這件事共有種不同方法。

乘法原理：完成一件事需要分成個步驟；完成第一步有種不同的方法，完成第二步有種不同的方法，…完成第步有種不同的方法；那么完成這件事共有種不同的方法。

解題關鍵：題干信息變化萬千但不離其宗，我們需要從其中提取出關鍵的數學信息，用邏輯思維進行整合判斷。將所有的題目拆解為“選取”和“排序”的過程，據此寫對應表達式。

考向1 相鄰問題——捆綁法：題目中規定某些元素必須相鄰，解題時當作一個大元素來進行排列。

注意：較復雜題目有存在多個大元素的情況。

例題：第一中學甲班的6名學生一起去大劇院觀看表演，安排有A、B兩排座位，每排3個位置。其中小明和小紅坐在一起的排法有（??）種。

A. 48 B. 96 C. 120 D. 168 E. 192

【答案】E

【解析】A排：①②③??B排：④⑤⑥

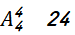小明和小紅必須要坐在一起，他們只能坐①②、②③、④⑤、⑤⑥，共有種，其他四名同學在剩下四個位置排序種，故共有種。

考向2 相離問題——插空法：元素相離（即不相鄰）問題，可先把無位置要求的幾個元素全排列，再把規定的相離的幾個元素插入上述幾個元素的空位和兩端。

例題：7人站成一排照相，若要求甲、乙、丙不相鄰，則有（??）種不同的排法。

A. 1020 B. 1040 C. 1140 D. 1220 E. 1440

【答案】E

【解析】除去甲、乙、丙三人余下四個人站位圖：①A②B③C④D⑤，他們之間有①②③④⑤種空位可以分別插入甲、乙、丙三人，則有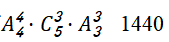種。

如果相鄰與相離問題同時出現，則先考慮相鄰元素，最后考慮相離元素。

考向3 隔板法：利用假定的隔板解決相同元素的分配問題。

題干標準形式一般表述為：將n個相同的元素分給個不同的對象，每個對象至少1個元素，求一共有多少種分法。

解題方法：將n個相同的元素排成一排，之間有n-1個空位，插入m-1塊隔板就可以分成m份，最后共有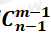種分法。

例題：趙一的媽媽來學校探望他，帶了一籃香蕉讓他和好朋友們共同分享。香蕉一共9支，分給寢室內包含趙一在內的四人，需保證每人至少有一支，那么總共有（??）種不同的分法。

A. 40 B. 48 C. 56 D. 64 E. 72

【答案】C

【解析】利用隔板法，最后答案為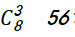種。

考向4 方冪法

審題重點：題干信息需要區分“可重復元素”和“不可重復元素”兩類元素。

解題方法：一共有“可重復元素不可重復元素”種情況，即“可重復元素”為底數，“不可重復元素”為指數。

例題：從甲市到乙市的大巴上共有20人，沿途共7個停靠點（包括乙市在內），則不同的下車方法共有（??）種。

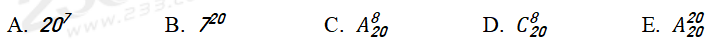
【答案】B

【解析】第1個人下車有7種方法，第2個人下車有7種方法……故總共有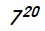種方法。

溫馨提示：文章由作者233網校-chenjing獨立創作完成，未經著作權人同意禁止轉載。