2024年考研備考已經開始,233網校考研上岸君給大家整理了考研數學高頻重難考點,供大家學習,建議收藏。
可分離的微分方程、齊次微分方程、齊次一階線性微分方程、非齊次一階線性微分方程。
可分離的微分方程:
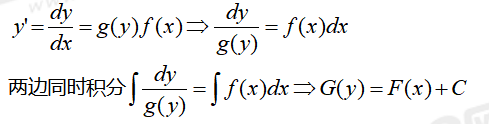
齊次微分方程:
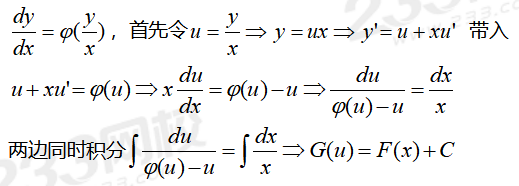
齊次一階線性微分方程:
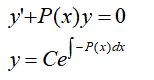
齊次一階線性微分方程:
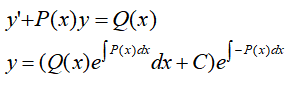
直角坐標系下二重積分與極坐標下的二重積分,直角坐標系下二重積分分兩種:一種是是X型。一種是Y型。
X型:設積分區域D:a≤x≤b,φ1(x)≤y≤φ2(x),如圖所示,φ1(x),φ2(x)在區間[a, b]上連續。
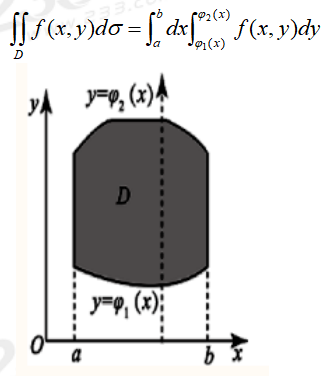
Y型:設積分區域D:c≤y≤d,?1(y)≤y≤?2(y),如圖所示,?1(x),?2(x)在區間[c, d]上連續。
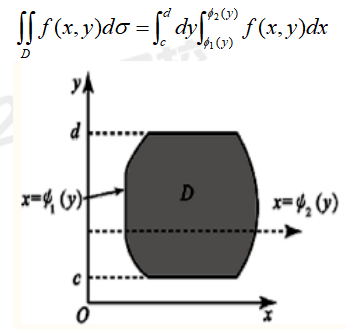
極坐標下的二重積分:由極坐標變換,設x=rcosθ,y=rsinθ,若積分區域D,則:

①如果積分區域D關于x軸對稱,則

其中D1為D的上半平面的部分。
②如果積分區域D關于y軸對稱,則

其中D2為D載右半平面的部分
③如果積分區域D關于y=x對稱,則
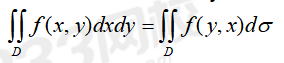
④如果積分區域D1,D2關于直線y=x對稱,則
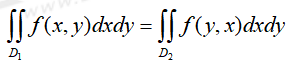
⑤如果積分區域D關于直線y=x對稱,則
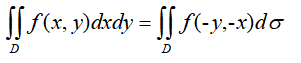
二元函數f(x,y)極值存在的必要條件:設函數f(x,y)在點(x0,y0)處偏導數存在,且在點(x0,y0)處取得極值,則f'x(x0,y0)=0, f'y(x0,y0)=0。
二元函數極值的求解方法:先f(x,y)對x,y分別求出偏導并令他們等于0
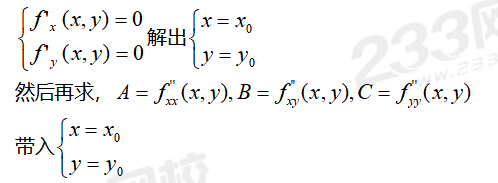
(1)AC-B2>0時,極值存在,且當A<0時有極大值,當A>0時有極小值。
(2)AC-B2<0時,極值不存在。
用拉格朗日法:
首先,構造拉格朗日函數F(x,y)=f(x,y)+λφ(x,y),

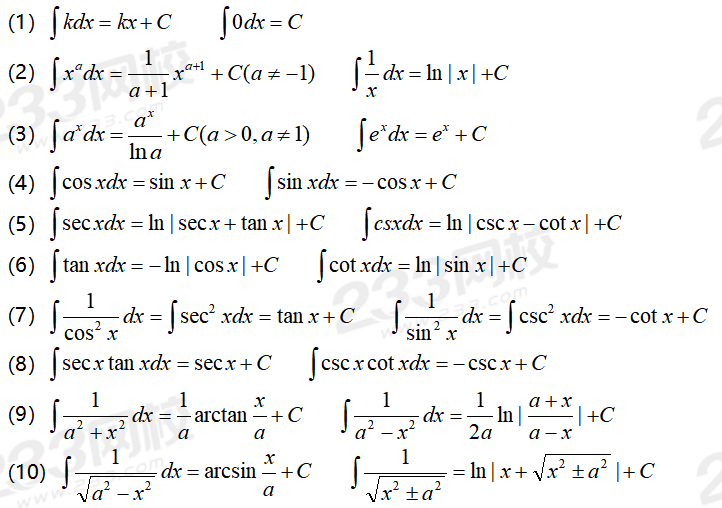

性質1 f(x)在區間[a, b]上可積的必要條件是f(x)在區間[a, b]上有界。
性質2 f(x)可積的充分條件有如下三個:
(i)若f(x)在區間[a, b]上連續,則f(x)在[a, b]上可積
(ii)若f(x)在區間[a, b]上有界,除有限個間斷點外函數連續,則f(x)在[a, b]上可積
(iii)若f(x)在區間[a, b]上單調,則f(x)在[a, b]上可積。
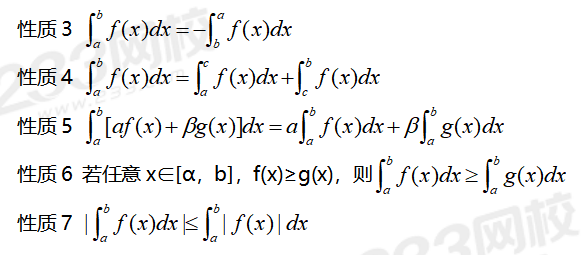
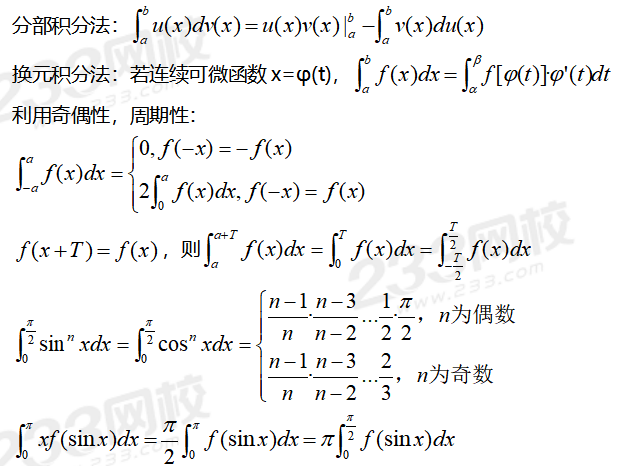
費馬定理:設函數y=f(x)在點x0的某領域U(x0)內有定義,且在x0處可導,若對任一x∈U(x0),有f(x)≤f(x0)或f(x)≥f(x0),則f’(x0)=0。
羅爾定理:設函數y=f(x)在閉區間[a,b]上連續,在開區間(a,b)內可導,且f(a)=f(b),則至少存在一點ξ∈(a,b),使得f’(ξ)=0。
拉格朗日中值定理:設函數y=f(x)在閉區間[a,b]上連續,在開區間(a,b)內可導,則至少存在一點ξ∈(a,b),使得f(b)-f(a)=f’(ξ)(b-a)。
柯西中值定理:設函數f(x),g(x)在閉區間[a,b]上連續,在開區間(a,b)內可導,且對任一x∈(a,b),g’(x)≠0,則至少存在一點ξ∈(a,b),使得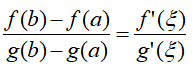 。
。
零點定理:設函數f(x)在閉區間[a,b]上連續,且f(a)與 f(b)異號(即f(a)× f(b)<0),那么在開區間(a,b)內至少有函數f(x)的一個零點,即至少有一點ξ(a<ξ<b)使f(ξ)=0。
介值定理:設函數f(x)在閉區間[a,b]上連續,且在這區間的端點取不同的函數值,f(a)=A及f(b)=B,那么,對于A與B之間的任意一個數C,在開區間(a,b)內至少有一點ξ,使得f(ξ)=C (a<ξ<b)。
泰勒定理:設函數y=f(x)在閉區間[a,b]上有連續的n階倒數,在開區間(a,b)內有n+1階倒數,則對任一x∈(a,b),有

第一種判定方法:設函數y=f(x)在x0處連續,且在x0的某去心領域U(x0,δ)內可導
(1)若當x∈(x0-δ,x0)時,f’(x)>0,而當x∈(x0,x0+δ)時,f’(x)<0,則f(x)在x0處取得極大值.
(2)若當x∈(x0-δ,x0)時,f’(x)<0,而當x∈(x0,x0+δ)時,f’(x)>0,則f(x)在x0處取得極小值.
(3)若當x∈U(x0,δ)時,f’(x)符號保持不變,則f(x)在x0處無極值.
第二種判定方法:設函數y=f(x)在x0處有二階導數且f’(x0)=0,f”(x)≠0,則
(1)當f”(x)<0時,函數y=f(x)在x0處取得極大值
(2)當f”(x)>0時,函數y=f(x)在x0處取得極小值
設函數y=f(x)在[a,b]上連續,在(a,b)內有一階和二階導數,則
(1)若在(a,b)內f”(x)>0,則函數y=f(x)在[a,b]上的圖形是凹的
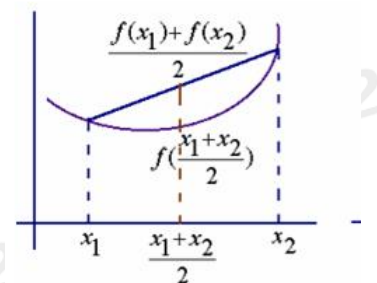
(2)若在(a,b)內f”(x)<0,則函數y=f(x)在[a,b]上的圖形是凸的
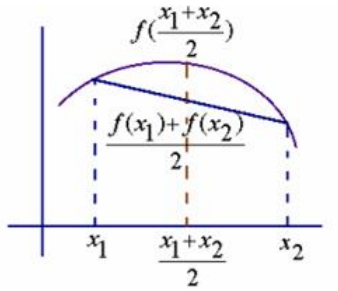

常見的初等函數的n階導數公式:



溫馨提示:文章由作者233網校-chenjing獨立創作完成,未經著作權人同意禁止轉載。
