大題考察的內(nèi)容大致可以分為9-11個(gè)類型,每年從中選出六個(gè)考察,有時(shí)候又會(huì)聯(lián)合出題,例如定積分+微分方程,積分+極限等,綜合性較強(qiáng),除了最后一個(gè)題線性代數(shù)不變之外,其他的內(nèi)容都是輪流考察的,這也是為什么老師講課都是分模塊,主要是各個(gè)擊破,我們首先要基礎(chǔ)打牢固,然后將所有的類型通過(guò)試題,多次訓(xùn)練,高分就會(huì)很穩(wěn)定。
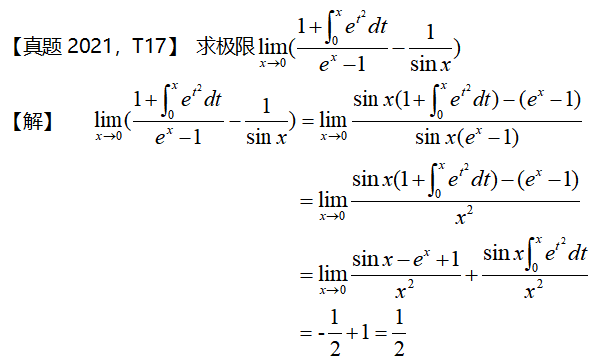
解題知識(shí)儲(chǔ)備:
1.洛必達(dá)法則
2.帶佩亞諾余項(xiàng)的泰勒公式如下:
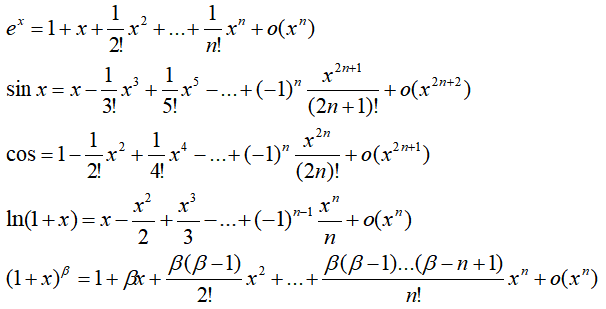

解題知識(shí)儲(chǔ)備:
二元函數(shù)極值存在的充分條件

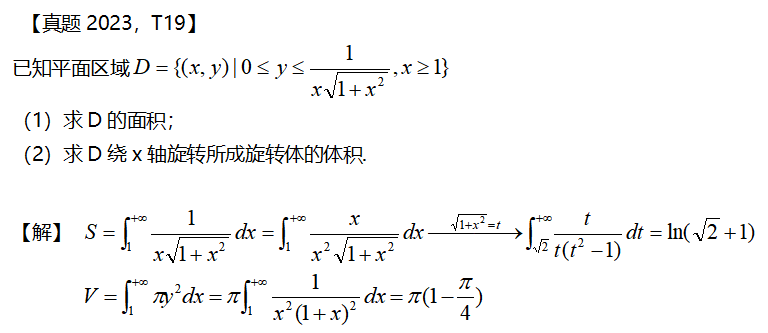
解題知識(shí)儲(chǔ)備:
繞x軸旋轉(zhuǎn)生成的旋轉(zhuǎn)體的體積
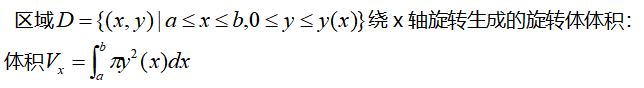
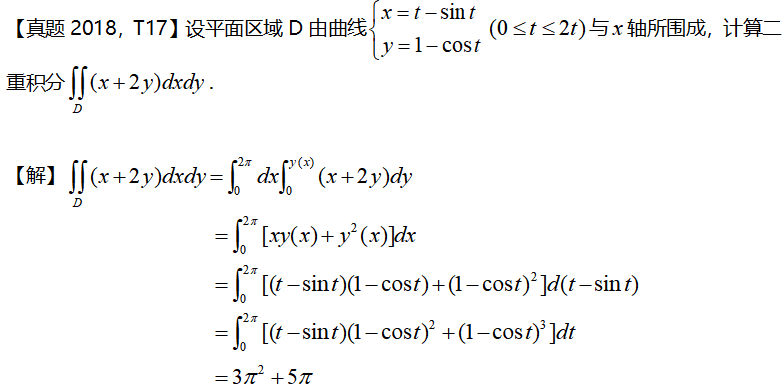
解題知識(shí)儲(chǔ)備:
二重積分,一是理解定義,二呢學(xué)會(huì)畫圖,三善于利用性質(zhì),
本題算數(shù)學(xué)二,二重積分較難考題了,主要是寫不出f(x)的函數(shù)表達(dá)式,掌握此題,二重積分沒有難題。


解題知識(shí)儲(chǔ)備:
只含有一個(gè)ε,無(wú)其他字母的中值定理的解法,及輔助函數(shù)的構(gòu)造方法。


解題知識(shí)儲(chǔ)備:
1.矩陣的等價(jià)
定義:設(shè)A與B均為m×n矩陣.如果矩陣A經(jīng)過(guò)有限次初等變換可以化為矩陣B,則稱矩陣A與B等價(jià).
2. 非齊次線性方程組解集的結(jié)構(gòu)

解題知識(shí)儲(chǔ)備:
極值的第一充分條件:


解題知識(shí)儲(chǔ)備:
二階常系數(shù)線性微分方程求解:



解題知識(shí)儲(chǔ)備:
1.數(shù)學(xué)歸納法
2.由單調(diào)有界準(zhǔn)則:?jiǎn)握{(diào)遞減有下界,數(shù)列收斂;