債券的價值分析可謂是占據了基金從業基礎知識計算題的半壁江山,零息票債券估值法、固定利率債券估值法、當期收益率、到期收益率、債券久期等等。沒有哪次基金從業考試會看不到它們。
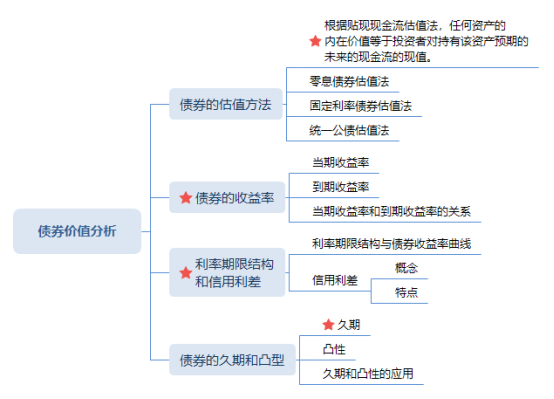
一、思維導圖結構梳理
二、三星考點精講
1、債券的估值方法
(1)零息債券估值法
零息債券通常以低于面值的貼現方式發行,不支付利息,到期按債券面值償還。(比如面值為100,發行價為90,到期按面值100償還)零息債券的內在價值為:
V=M/(1+r)t
V表示零息債券的內在價值;
M表示面值;
r表示年化市場利率;
t表示債券到期時間(單位:年)
例:某種貼現式國債面額為100元,貼現率為5%,到期時間為120天,則該國債的內在價值為100×(1-120/360×5%)=98.33【多數零息債券小于1年,應根據實際計息日進行計算】
(2)固定利率債券估值法
固定利率債券式一直按照票面金額計算利息,票面上附有(可不附有)作為定期支付利息憑證的期票的債券。

V表示固定利率債券的內在價值;
C表示每期支付的利息;
M表示面值;
r表示市場利率;
n表示債券到期時間。
(3)統一公債
統一公債是一種沒有到期日的特殊債券,其內在價值的計算為:V=C/r。
2、債券的收益率
(1)當期收益率
債券的當期收益率是債券的年利息收入與當前的債券市場價格的比例。
計算公式為:I=C/P,I表示當前收益率;C表示年息票利率;P表示債券市場價格。
(2)到期收益率
到期收益率又稱內部收益率,是可以使投資購買債券獲得的未來現金流的現值等于債券當前市價的貼現率。隱含兩個重要假設:①投資者持有至到期;②利息再投資收益率不變。債券市場價格和到期收益率的關系為:
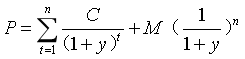
P表示債券市場價格;
C表示每期支付的利息;
n時期數;
M債券面值。
注意:到期收益率的公式和上面固定利率債券估值的公式其實是一樣的。
由公式可以看出,影響到期收益率的因素由以下四個:①票面利率;②債券市場價格;③計息方式;④再投資收益率。
【精選?真題演練】
票面金額為100元的3年期債券,票面利率5%,每年付息一次,當前市場價格為90元,則該債券的到期收益率為( )。
A. 8.9468%
B. 5.0556%
C. 1.7235%
D. 5%
(3)債券當期收益率和到期收益率的關系
①債券市場價格越接近債券面值,期限越長,則當期收益率就越接近到期收益率;
②債券市場價格越偏離債券面值,期限越短,則當期收益率就越偏離到期收益率。
3、利率期限結構和信用利差
利率期限結構是指在某一時點上,各種不同期限債券的收益率和到期期限之間的關系。分為四種類型:
①上升收益率曲線(特征:短期債券收益率較低,長期債券收益率較高)
②反轉收益率曲線(特征:短期債券收益率較高,長期債券收益率較低)
③水平收益率曲線(特征:長短期債券收益率基本相等)
④拱形收益率曲線(特征:期限相對較短的債券,利率與期限成正向關系,期限較長的債券,利率與期限呈反向關系)
信用利差:指除了信用評級不同外,其余條件全部相同的兩種債券收益率的差額。
4、債券的久期和凸性
(1)債券久期
債券本息所有現金流的加權平均到期時間,即債券投資者收回其全部本金和利息的平均時間。計算公式為:
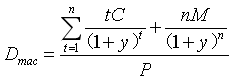
Dmac=麥考利久期,P=債券價格,C=每次付息金額,M=債券面值,n=付息周期數;t=期數。修正的麥考利久期等于麥考利久期除以(1+y)。
【精選?真題演練】
1、某2年期債券的面值為1000元,票面利率為6%,每年付息一次,現在市場收益為8%,其市場價格為964.29元,則麥考利久期為( )。
A. 1.94年
B. 2.04年
C. 1.75年
D. 2年
2、該債券最可能采用(??)發行,發行之初麥考利久期為(??)。
A. 溢價;1.94年
B. 折價;2.16年
C. 溢價;2年
D. 折價;1.86年
(2)凸性
價格-收益率曲線的曲率就是債券的凸性。凸性意味著債券的價格-收益率曲線的斜率隨著收益率而變化。凸性導致債券收益率下降所引起的債券價格上升的幅度不等于收益率同比上升所引起的債券價格下降的幅度。
點擊視頻可試聽本章相關知識的講解,基礎打牢,證書跑不了!























