債券久期是基金從業(yè)考試的一個重難點，很多人在學(xué)習(xí)時會戰(zhàn)略性地放棄這個考點。但是這個點同時又是基金從業(yè)的高頻考點，其實基金從業(yè)考試時基本都是比較簡單的計算，能不丟分就別丟。本文從概念入手，將久期的計算過程進行拆分，幫助你理解債券的久期是怎么計算的。

一、債券久期的概念

美國學(xué)者麥考利將久期定義為債券本息所有現(xiàn)金流的加權(quán)平均到期時間，也就是債券的投資者收回其全部本金和利息的平均時間。因為債券的到期時間不能全面反映所有債券的期限特性。

借用教材上的例子：A息票率5%的10年期債券和B年利率為5%的10年期零息債券，它們的現(xiàn)金流分別是怎樣的呢？

A：每年產(chǎn)生的現(xiàn)金流——債券面值的5%+到期還本

B：持有期間不產(chǎn)生任何現(xiàn)金流，到期還本付息。（零息債券一般在一年/一年以內(nèi)，以低于債券面值的價格發(fā)行，到期支付債券面值，其中的差額即為投資者收益）

由A和B現(xiàn)金流的對比，我們可以看到，A債券在持有期間可以產(chǎn)生多次現(xiàn)金流，而B零息債券僅到期還本付息一次。A的每筆現(xiàn)金流都可以進行再投資，所以直接按最后歸還本金的期限來計算債券的到期期限是沒有辦法反映債券的期限特性的。這時再看債券久期的定義就更能理解了。

二、債券久期的計算公式

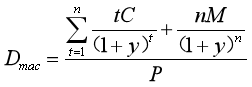
P：債券價格

C：付息金額

y：應(yīng)計收益率

N：付息周期數(shù)

M：面值

T：期數(shù)

基金從業(yè)考試時，基本只要記住這個公式，知道每個字母代表的意思就可以做出來了，不繞彎。但是我們還是可以梳理一下麥考利久期的計算思路，幫助理解記憶，考試時不套公式能按這個步驟也可以算出答案。麥考利久期的計算過程可以簡單地分為三步：

①計算每次支付金額的現(xiàn)值占當前債券價格的比率；

每期支付金額的現(xiàn)值為：C/(1+y)、C/(1+y)²、C/(1+y)³...C/(1+y)^t，以及到期返還的債券面值M/(1+y)ⁿ，分別除以價格P即算出每次支付金額的現(xiàn)值占當前債券價格的比率為C/(1+y)/P、C/(1+y)²/P、C/(1+y)³/P...C/(1+y)^t/P，以及到期返還的債券面值M/(1+y)ⁿ/P。

②以第一步計算出來的比率為權(quán)重，乘以每次支付的期限，得到每次支付的加權(quán)期限；

1C/(1+y)/P、2C/(1+y)²/P、3C/(1+y)³/P...tC/(1+y)^t/P，以及到期返還的債券面值nM/(1+y)ⁿ/P

③將第二步計算出來的加權(quán)期限加總，得到債券的久期。

三、修正久期

麥考利久期處以（1+y）被定義為修正久期：D_mod=D_mac/(1+y)

在給定收益變化下，債券價格的百分比變化與修正久期變化方向相反。修正久期越大，由給定收益率變化引起的價格變化越大。