本文主要寫道幾個現(xiàn)代投資理論的內(nèi)容：均值——方差模型，資產(chǎn)收益率的期望、方差和協(xié)方差以及最小方差前沿與有效前沿。教材中對于這塊內(nèi)容寫得不深，要求我們對相關(guān)概念有所了解。

均值——方差模型

均值方差模型是馬科維茨提出的風(fēng)險度量模型。揭示了“資產(chǎn)的期望收益由其自身的風(fēng)險的大小來決定”這一結(jié)論。

 均值——方差模型的假設(shè)

（1）投資者在考慮每一次投資選擇時，其依據(jù)是某一持倉時間內(nèi)的證券收益的概率分布。

（2）投資者是根據(jù)證券的期望收益率估測證券組合的風(fēng)險。

（3）投資者的決定僅僅是依據(jù)證券的風(fēng)險和收益。

（4）在一定的風(fēng)險水平上，投資者期望收益最大；相對應(yīng)的是在一定的收益水平上，投資者希望風(fēng)險最小。

 資產(chǎn)收益率的相關(guān)概念

期望：期望收益率是收益率的期望值，資產(chǎn)各種可能收益率的加權(quán)平均值。設(shè)E(rp)為投資組合的期望收益率，E(ri)為第i個資產(chǎn)的收益率，wi為第i個資產(chǎn)的權(quán)重，n為資產(chǎn)數(shù)目，那么投資組合期望收益率為：

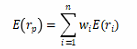
方差和標(biāo)準(zhǔn)差：方差和標(biāo)準(zhǔn)差是估計(jì)資產(chǎn)實(shí)際收益率與期望收益率之間可能偏離程度的測度方法。對于單一資產(chǎn)，其收益方差和標(biāo)準(zhǔn)差計(jì)算公式：

方差：

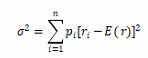
標(biāo)準(zhǔn)差：

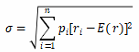
σ²為方差；σ為標(biāo)準(zhǔn)差；ri表示該資產(chǎn)在第i種狀態(tài)下的收益率；pi表示收益率ri發(fā)生的概率；n表示資產(chǎn)可能的收益狀態(tài)的總數(shù)；E(r)表示該資產(chǎn)的期望收益率。

協(xié)方差和相關(guān)關(guān)系:

在投資組合理論中使用協(xié)方差和相關(guān)系數(shù)測度兩個風(fēng)險資產(chǎn)的收益之間的相關(guān)性。兩個資產(chǎn)收益率的相關(guān)型系數(shù)定義為協(xié)方差除以兩個證券各自標(biāo)準(zhǔn)差的乘積。相關(guān)系數(shù)的取值范圍是[-1，+1]

當(dāng)P>0時，兩變量為正線性相關(guān)；

當(dāng)ρ<0時，兩變量為負(fù)線性相關(guān)；

當(dāng)ρ=0時，兩變量間無線性相關(guān)關(guān)系。

|ρ|越接近1，表示兩變量間線性關(guān)系越密切；|ρ|越接近于0，表示兩變量的線性相關(guān)越弱。當(dāng)|ρ|=1時，表示兩變量為完全線性相關(guān)。

最小方差前沿與有效前沿

本知識點(diǎn)在出題時主要出在以下幾個點(diǎn)：

（1）可行集：市場上可投資所形成的所有組合，又稱機(jī)會集。 

（2）有效前沿是能夠達(dá)到的最優(yōu)的投資組合的集合，它位于所有資產(chǎn)和資產(chǎn)組合的左上方。

（3）無差異曲線特點(diǎn)：

①風(fēng)險厭惡的投資者的無差異曲線是從左下方向右上方傾斜的。

②同一條無差異曲線上的所有點(diǎn)向投資者提供了相同的效用。

③對于給定風(fēng)險厭惡系數(shù)A的某投資者來說，可以畫出無數(shù)條無差異曲線，且這些曲線不會交叉。

④當(dāng)向較高的無差異曲線移動時，投資者的效用增加。

⑤風(fēng)險厭惡程度高的投資者與風(fēng)險厭惡程度低的投資者相比，其無差異曲線更陡，因?yàn)殡S著風(fēng)險增加，其要求的風(fēng)險溢價更高。