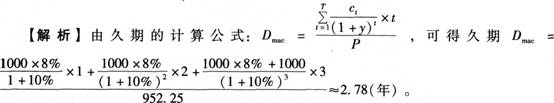基金從業資格考試《證券投資基金基礎知識》科目中涉及投資基礎知識，涉及少量計算題。考試大綱中要求掌握債券久期(麥考利久期和修正久期)的概念、計算方法和應用。基金計算題真題專項講解>>
掌握債券久期(麥考利久期和修正久期)的概念，理解公式的原理，計算題也不難。
麥考利久期的概念
為了全面反映債券現金流的期限特性，美國學者麥考利(Macaulay)于1938年引入久期(Duration)概念。
麥考利久期是使用加權平均數的形式計算債券的平均到期時間。它是債券在未來產生現金流的時間的加權平均,其權重是各期現值在債券價格中所占的比重。
對于零息債券，其久期等于到期期限;對于附息債券，在債券到期之前的每一次付息都會縮短加權平均到期時間，因此付息時間的提前或者付息金額的增加都會使債券的久期縮短。
麥考利久期的 公式
麥考利久期的計算過程是計算每次支付金額的現值占當前債券價格的比率，然后以此比例為權重，乘以每次支付的期限，得到每次支付的加權期限，再將每次的加權期限加總，即得到債券的久期。
其中：P為債券價格；C為每次付息金額；y為每個付息周期應計收益率(半年付息即為年化收益率的一半)；n為付息周期數(半年付息一次時為年數× 2)；M為面值。
麥考利久期的例題
1.某2年期債券，每年付息一次，到期還本，面值為100元，票面利率為10%，市場利率為10%，則該債券的麥考利久期為(??)年。
A.1.35
B.1.73
C.1.91
D.2.56
參考答案：C
參考解析：市場利率=票面利率，則該債券的現值=面值=100(元)，第一年現金流現值=100×10%/(1+10%)≈9.09(元)，第二年現金流現值=(100×10%+100)/(1+10%)2≈90.91(元)，因此，麥考利久期D=1×9.09/2×90.91/100=1.91(年)。
2.某3年期債券的面值為1000元，票面利率為8%，每年付息一次，現在市場收益率為10%，其市場價格為950.25元，則其久期為()。
A.2.78年
B.3.21年
C.1.95年
D.1.5年
參考答案：A
參考解析：
